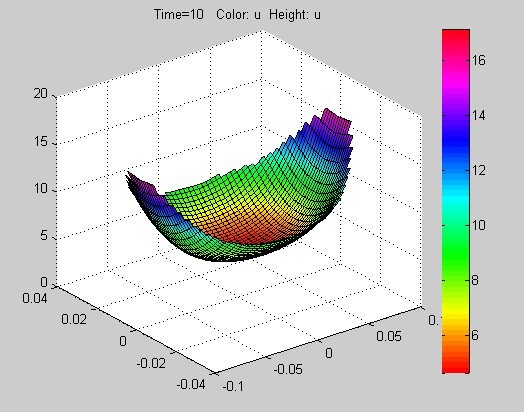
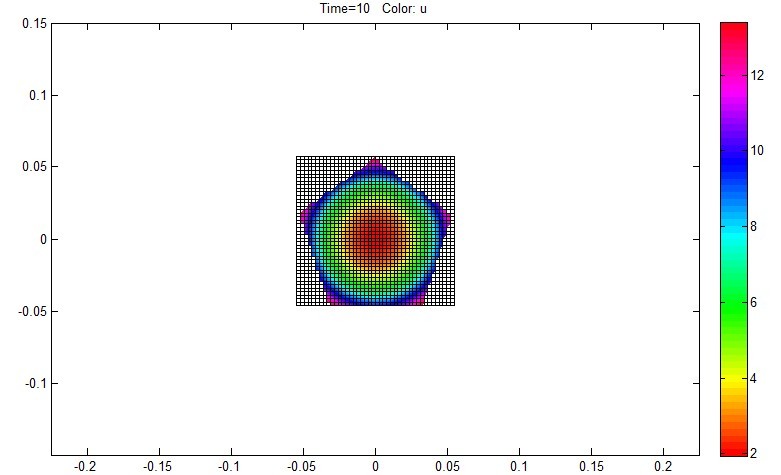
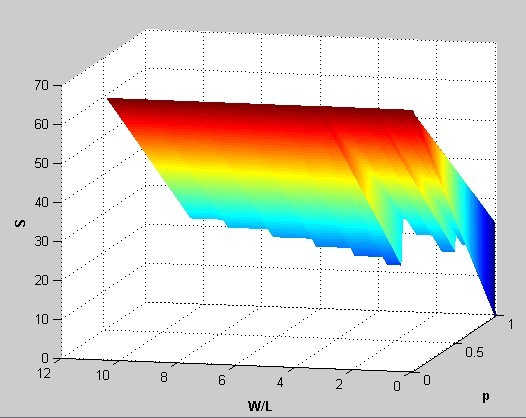
We chose Problem A in the contest to find the optimum choice of Browne pan's shape and the ratio of width and length (W/L) in oven in order to get more food evenly heated. We built two models - one to verify the distribution of heat transfer process in pans of different shapes (round, ellipse, triangle, square, pentagon) and one to find the optimum shape of pan in the oven.

We found oval pan had the largest area of being evenly heated when all pans have the same area. Based on the second model, we chose rectangular oven as the best one for largest area of evenly heating. We suppose that several oval pans put in two rows in the oven could be the optimum choice.

We got Meritorious Winner Award (10%) in The Mathematical Contest in Modeling of America 2013.